OPENING QUESTION: Let's Review:

• How is your weight different from your mass?

Answer → Your mass is determined by the number of atoms that make up your body. Your weight is how much the gravity of whatever planet (or moon etc...) is pulling on your mass-- mg

• How is Newton's 3rd soooo helpful in analyzing force problems?

Answer → Newton's 3rd helps us identify forces - especially when we use the NVN (noun verb noun) format. That's particularly useful in odd situations such as air friction (I hit air molecules, air molecules hit me)

• Newton's 2nd is particularly helpful in finding.... what?

Answer → Newton's 2nd is helpful in finding "How Much" using F = ma

• Newton's 1st helps us keep in mind that objects do... what?

Answer → Whatever the forces tell them to do. If forces balance, the object doesn't do anything different. If the forces are not balanced, an object will accelerate in the direction of that unbalanced force.

• What is the key to dealing with hanging problems?

Answer → Componentize your vectors... always

• There is only ONE force that starts the ball rolling (so to speak) on ramp problems, what might that be?

Answer → The weight of the object sliding down the ramp is key (mg). The component of that force, mgsingθ, attempts to pull the object down the ramp. If friction is present, the Normal force is found using the component of force given by mgcosθ

• What are its component forces

Answer → see above

Brain Befuddlement:

If we define your weight as your mass being pulled to the center of the Earth by gravity, it doesn't change in an elevator (or indeed, anywhere on the surface of the Earth).

However, if we define your weight as the force exerted by the floor of an elevator as it accelerates you upwards or downwards then, yes, your weight changes.

What gives?

Answer → mama Earth will ALWAYS try to pull objects to her center. That means mg ALWAYS applies. How strongly that pull is resisted results in the force that we feel such as the floor of the elevator or the back of the seat cushion pushing up on us in the capsule of a rocket.

═══════════════════════════

FORMULAE OBJECTUS:

Newton's Second: F = ma

Newton's Second (weight): w = mg

Newton's First/Second analytics: ∑F_x = ma_x ;∑F_y = ma_y

LEARNING TARGET: I will be able to complete elevator problems during today's class.

I will review hanger problems today.

I will review ramp problems today.

WORK O' THE DAY:

Consider the following situation:

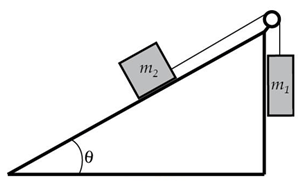
What forces are working to pull the object m₂ down the ramp (please be specific)?

Answer → mgsinθ

What forces are working against the object m₂ sliding down the ramp (please be specific)?

Answer → friction between m₂ and the ramp and the weight of m₁

If object m₁ is accelerating downwards, what can we say about friction?

Answer → fThat friction between m₂ and the block is not great enough to overcome the weight of m₁

How would you go about writing a "sum of the forces" equation for that situation?

Answer →

∑_dtr = ma_dtr

Now list ALL forces in the down-the-ramp orientation (don't worry about signs, we'll deal with them in a moment):

m₂gsinθ + f + m₁g = ma_dtr

We don't know anything about the situation (whether it is at rest, what the masses are etc...) so we don't know if friction is positive or negative until we know which direction m₂ is sliding so let's just leave it alone for now.

We *do* know that m₂ and m₁ are pulling against each other, so let's just go ahead and define m₁ as pulling "down" and make it negative:

m₂gsinθ + f - m₁g = ma_dtr

And here's a bit of interesting info, we have two masses. Each mass will be influenced by the forces acting on the system as a whole, so we do our final change to the sum-of-the-forces equation:

m₂gsinθ + f - m₁g = ma_dtr

And that's all we can do until we learn more about the system!

m₂gsinθ + f - m₁g = (m₁+ m₂)(a_dtr)

Y*I*K*E*S!

═══════════════════════════

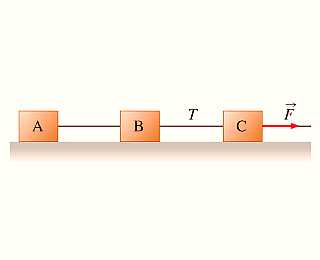
Let's say some sort of applied force is exerted to the left on the boxes shown above as accelerate across a frozen hockey rink.

Do a Newton's 1st on that situation.

Answer → The applied force treats objects A, B and C as ONE mass with the combined mass of all 3 objects:

F_app = (m_A + m_B + m_C)(a)

Determine the acceleration of box C.

Answer →

F_app = (m_A + m_B + m_C)(a)

F_app/(m_A + m_B + m_C) = (a)

Now let's say they are made of different materials and are dragged across a surface that is NOT friction free.... do a sum-of-the-forces on THAT beastie

Answer →